|
一.PCA
PCA通过正交变换将一组由线性相关变量表示的数据转换为少数几个由线性无关变量表示的数据,这几个线性无关的变量就是主成分。PCA通过将高维数据维度减少到少数几个维度,本质上属于一种数据降维方法,也可以用来探索数据的内在结构。



可看出如果两个随机变量的分布相似,它们的协方差很大。



import numpy as np
class PCA():
# 计算协方差矩阵
def calculate_covariance_matrix(self, X):
m = X.shape[0]
# 数据标准化
X = X - np.mean(X, axis=0)#(x1 - Ex1) (x2 - Ex2)
return 1 / m * np.matmul(X.T, X)
def compute_feature(self, X, n_components):
# 计算协方差矩阵
covariance_matrix = self.calculate_covariance_matrix(X)
print('==covariance_matrix:', covariance_matrix.shape)
# 计算协方差矩阵的特征值和对应特征向量
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
print('=eigenvectors.shape:', eigenvectors.shape)
# 对特征值排序
idx = eigenvalues.argsort()[::-1]
# 取最大的前n_component组
eigenvectors = eigenvectors[:, idx]
eigenvectors = eigenvectors[:, :n_components]
# Y=PX转换
return np.matmul(X, eigenvectors)
#两个样本 一个样本有三维
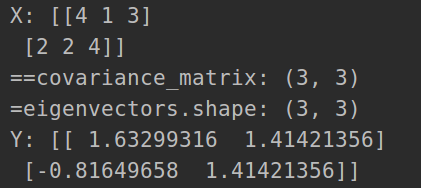
X = np.array([[4, 1, 3],
[2, 2, 4]])
print('X:', X)
pca = PCA()
Y = pca.compute_feature(X, 2)#降到2维
print('Y:', Y)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
def plot_digits(images, y, max_n=10):
"""
显示手写数字的图像
"""
# 设置图像尺寸
fig = plt.figure(figsize=(2. * n_col, 2.26 * n_row))
i = 0
while i < max_n and i < images.shape[0]:
p = fig.add_subplot(n_row, n_col, i + 1, xticks=[], yticks=[])
p.imshow(images[i], cmap=plt.cm.bone, interpolation='nearest')
# 添加标签
p.text(0, -1, str(y[i]))
i = i + 1
plt.show()
# 显示8*8数字
# plot_digits(digits.images, digits.target, max_n=10)
def plot_pca_scatter_three(digits, X_pca, y_digits, class_nums):
"""
主成分显示
"""
##显示3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(len(class_nums)):
# print('==y_digits == i:', y_digits == i)
print(X_pca[:, 0][y_digits == i].shape)
print(X_pca[:, 1][y_digits == i].shape)
print(X_pca[:, 2][y_digits == i].shape)
ax.scatter(X_pca[:, 0][y_digits == i], X_pca[:, 1][y_digits == i], X_pca[:, 2][y_digits == i], label = class_nums[i])
plt.legend(digits.target_names)
ax.set_xlabel('First Principal Component')
ax.set_ylabel('Second Principal Component')
ax.set_zlabel('Third Principal Component')
plt.savefig('./three.jpg')
plt.show()
def plot_pca_scatter_two(digits, X_pca, y_digits, class_nums):
# 显示2D
for i in range(len(class_nums)):
px = X_pca[:, 0][y_digits == i]
py = X_pca[:, 1][y_digits == i]
plt.scatter(px, py, label=class_nums[i])
plt.legend(digits.target_names)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.savefig('./two.jpg')
plt.show()
def pca_aysis_two_components():
digits = load_digits()
X_digits, y_digits = digits.data, digits.target
# n_row, n_col = 2, 5
print('=X_digits.shape:', X_digits.shape)
print('==y_digits:', y_digits[:10])
print(len(y_digits))
class_nums = [i for i in range(10)]
n_components = 2 # 取前2个主成分
pca = PCA(n_components=n_components)
# fit_transform表示做完训练以后并进行转换
X_pca = pca.fit_transform(X_digits)
print('==X_pca.shape:', X_pca.shape)
plot_pca_scatter_two(digits, X_pca, y_digits, class_nums)
def pca_aysis_three_components():
digits = load_digits()
X_digits, y_digits = digits.data, digits.target
print('=X_digits.shape:', X_digits.shape)
print('==y_digits:', y_digits[:10])
print(len(y_digits))
class_nums = [i for i in range(10)]
n_components = 3 # 取前2个主成分
pca = PCA(n_components=n_components)
# fit_transform表示做完训练以后并进行转换
X_pca = pca.fit_transform(X_digits)
print('==X_pca.shape:', X_pca.shape)
plot_pca_scatter_three(digits, X_pca, y_digits, class_nums)
if __name__ == '__main__':
# pca_aysis_two_components()
pca_aysis_three_components()

可视化二维的时候:

可视化三维的时候:

二.SVD

numpy案例
A = np.array([[4, 1, 3],
[2, 2, 4]])
print('A:\n', A)
# 对其进行SVD分解 s是对角矩阵的值
u, s, vt = np.linalg.svd(A, full_matrices=True)
print('u.shape, s.shape, vt.shape:', u.shape, s.shape, vt.shape)
res = np.dot(u*s, vt[:2, :])
print('res:', res)
#U UT=I
print('np.dot(u, u.T):\n', np.dot(u, u.T))
#v vT=I
print('np.dot(vt, vt.T):\n', np.dot(vt, vt.T))

将SVD用于图像的压缩算法。其原理就是保存像素矩阵的前k个奇异值,并在此基础上做图像恢复。由SVD的原理我们可以知道,在SVD分解中越靠前的奇异值越重要,代表的信息含量越大。
import cv2
import numpy as np
import os
from tqdm import tqdm
# 定义恢复函数,由分解后的矩阵恢复到原矩阵
def restore(u, s, v, K):
'''
u:左奇异矩阵 u uT=I
v:右奇异矩阵 v vT=I
s:奇异值矩阵 对角矩阵
K:奇异值个数
'''
m, n = len(u), len(v)
a = np.zeros((m, n))
for k in range(K):
uk = u[:, k].reshape(m, 1)
vk = v[k].reshape(1, n)
# 前k个奇异值的加总
a += np.dot(uk * s[k], vk)
a = a.clip(0, 255)
return np.rint(a).astype('uint8')
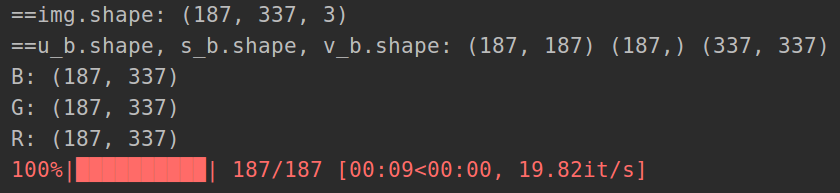
img = cv2.imread("./111.png")
print('==img.shape:', img.shape)
h,w,_ = img.shape
# 对RGB图像进行奇异值分解
u_b, s_b, v_b = np.linalg.svd(img[:, :, 0])
u_g, s_g, v_g = np.linalg.svd(img[:, :, 1])
u_r, s_r, v_r = np.linalg.svd(img[:, :, 2])
print('==u_b.shape, s_b.shape, v_b.shape:', u_b.shape, s_b.shape, v_b.shape)
B = np.dot(u_b * s_b, v_b[:h, :])
print('B:', B.shape)
G = np.dot(u_g * s_g, v_g[:h, :])
print('G:', G.shape)
R = np.dot(u_r * s_r, v_r[:h, :])
print('R:', R.shape)
# # 使用前短边个奇异值
K = min(img.shape[:2])
new_img = cv2.merge([B, G, R])
cv2.imwrite('./test_svd.jpg', new_img)
# # 恢复图像
ouput_path = './svd'
os.makedirs(ouput_path, exist_ok=True)
for k in tqdm(range(1, K + 1)):
B = restore(u_b, s_b, v_b, k)
R = restore(u_r, s_r, v_r, k)
G = restore(u_g, s_g, v_g, k)
new_img = cv2.merge([B, G, R])
cv2.imwrite(os.path.join(ouput_path, '{}.jpg'.format(k)), new_img)


|














